How to Draw a Concentric Circle

Using only a circumvolve and direct lines, it's possible to create diverse aesthetic curves that combine both art and mathematics. The geometry behind the concentric circle, ellipse, and cardioid dates back centuries and is easily found in the world around u.s.a.. From an archery target to an apple, tin can you name these geometric shapes?

You will by the stop of this step-by-step tutorial, and y'all'll also be ready to try your mitt at some geometric art yourself, which you could so spin into op art or string art. To create the curve examples that follow, I used a pencil, ruler, and protractor to marking off degrees and keep things exact. If you want, you could even use the free computer program GeoGebra to draw concentric circles, ellipses, and cardioids.

How to Create Concentric Circles, Ellipses, Cardioids & More Using Straight Lines & Circles — Concentric circles (top), ellipse (lesser left), and cardioid (bottom right). *Images past Cory Poole/WonderHowTo*

Materials & Tools Needed

For all of these curves, we'll need a few bones geometry tools and drawing utensils.

paper
ruler or direct border
pen or pencil
compass for drawing circles (or images of circles or regular polygons)
protractor (for marker off precise degrees)

Option 1. Making Concentric Circles

Concentric circles are circles that share a midpoint, such equally an archery target or a dartboard. The circles, though different size, all have the aforementioned bullseye. Regular polygons, regular polyhedra, and spheres can too be described as concentric as they all share the aforementioned eye. In fact, in our first case below, we create a concentric circle by cartoon polygons:

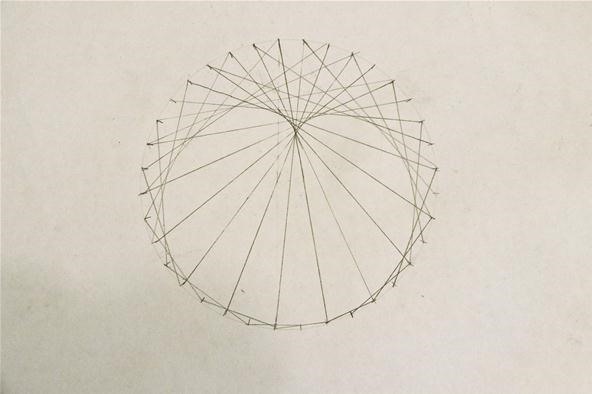
Step one: Mark a Circle at Even Intervals

This circle is marked every x degrees, then 36 marks total:

Step 2: Connect One Mark to Some other

The number of marks skipped volition determine the size of the concentric circle created. I chose to skip eight:

Step 3: Create Lines All the Way Around the Circle

Accept the adjacent mark and connect information technology to the mark ahead of the one you connected the previous one to. Continue doing this.

Based on your first mark, take the next marking and connect it to the mark ahead of the ane you connected the previous one to, then continue doing this:

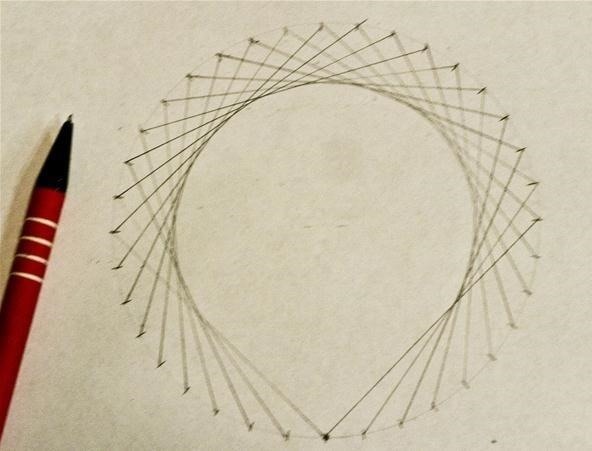
The resultant polygon has the same number of sides equally in that location were marks on the original circle:

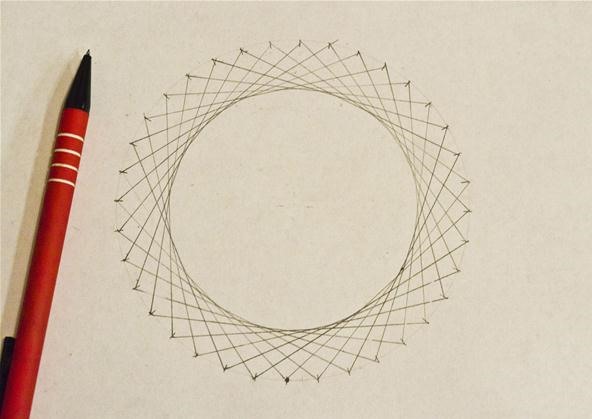
You can then utilise the within circle every bit a starting point for creating another circle:

These concentric circumvolve designs are really creating star polygons, every bit discussed in the posts on creating star designs on pumpkins and creating torus knots. In the prototype below, using GeoGebra (Classic), I took a circle with thirty marks and continued them in a design with six pentagrams. This works considering 30 / 5 = 6:

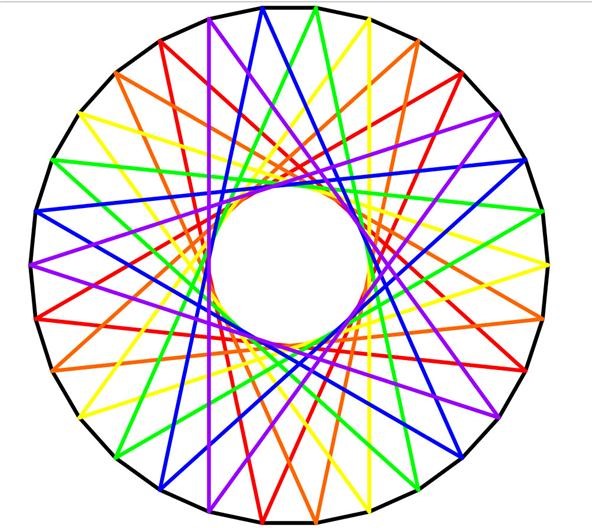
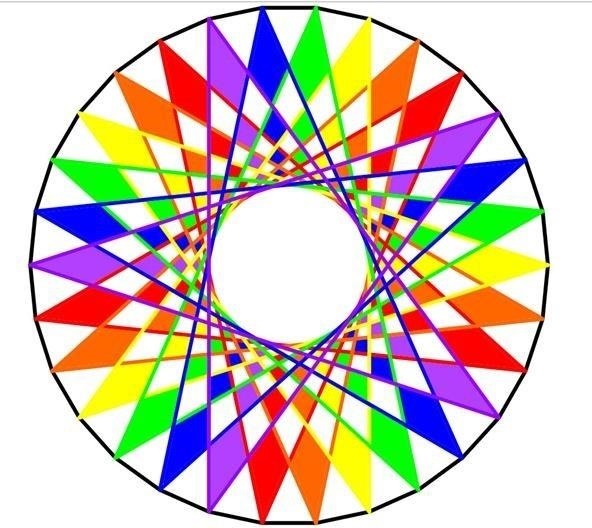
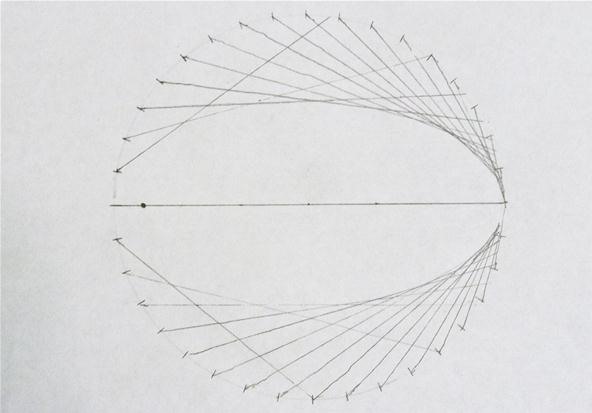
Option 2. Making Ellipses

Like the Earth's orbit effectually the Sun, an ellipse is a "closed curved shape that is apartment" and all-time described as an oval. This squashed circle has 2 focal points, where "the sum of the distances to the foci is constant for every signal on the curve."

Step i: Marker Off a Circle by Degrees

At that place are lots of ways to create ellipses, only this one is pretty fun. Start with a circle with a number of evenly spaced marks; I once more chose x degrees. I so connected 2 of the marks that were 180 degrees autonomously, halving the circumvolve. This line will become the major axis:

Step 2: Choose a Betoken on the Major Centrality

Mark a bespeak on your major axis. Making this point further from the heart of the circle makes the ellipse longer and narrower.

Step 3: Draw a Line from the Focal Point

Make a right bending on one of the marks on the circumvolve so that one of the sides of the angle goes through the focus. Connect the line from the marker to where it intersects the circle. Keep this procedure for all of the marks on the circle:

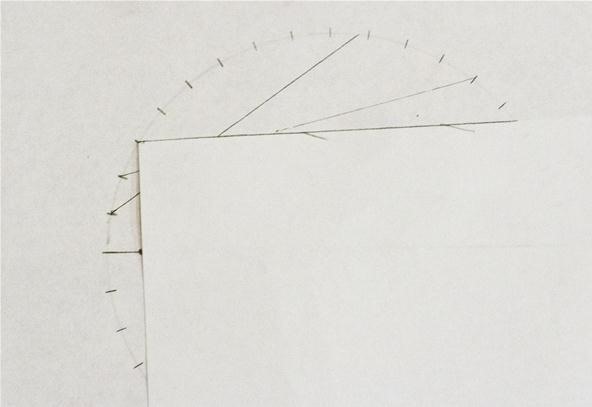
Halfway done; the resolution increases as it gets further from the focus:

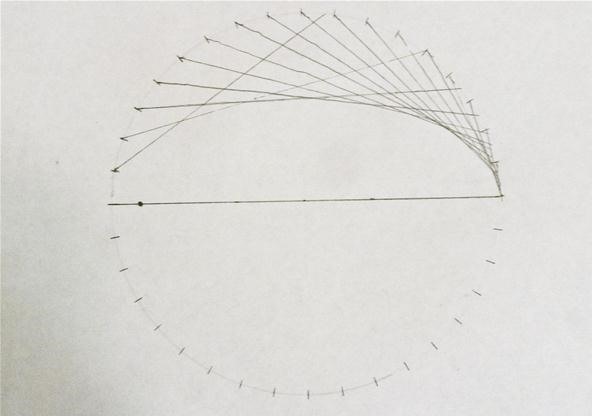
And hither is the completed ellipse. Note y'all could improve the resolution well-nigh the focus by repeating the process using the focus on the other side:

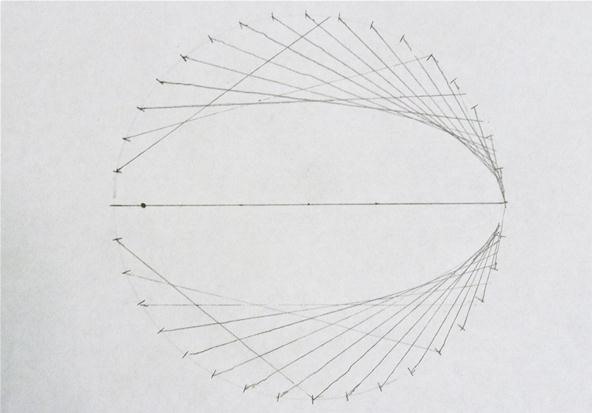
From the ellipse, I went a stride further and intersected 2 ellipses at right angles. The result was the following centre shape, a pattern that brought me to mind the bend in mathematics that is known for its middle-like shape, the cardioid, which will cover next.

Option 3. Making Cardioids

A cardioid is formed by a rolling circumvolve'south path across the circumference of another circle, all the while keeping its radius the aforementioned. The term, outset used in 1741 by Giovanni de Castillon (in Philosophical Transactions of the Majestic Lodge, 1741), originates from the Greek word for "heart." An everyday object that holds a true cardioid shape? An apple.

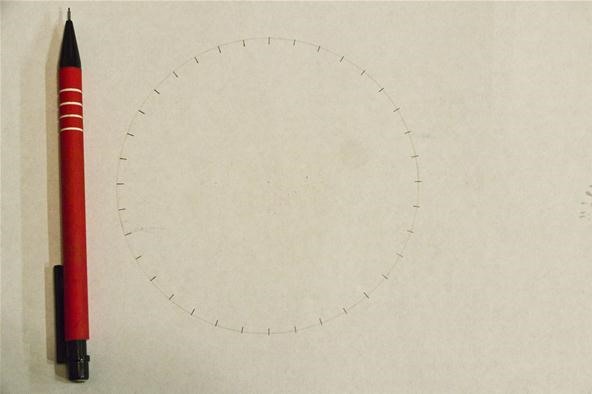
Step 1: Marking a Circle's Circumference Evenly

To create a cardioid, start with a circle with a number of evenly spaced marks; I chose every 10 degrees on this one all the same again:

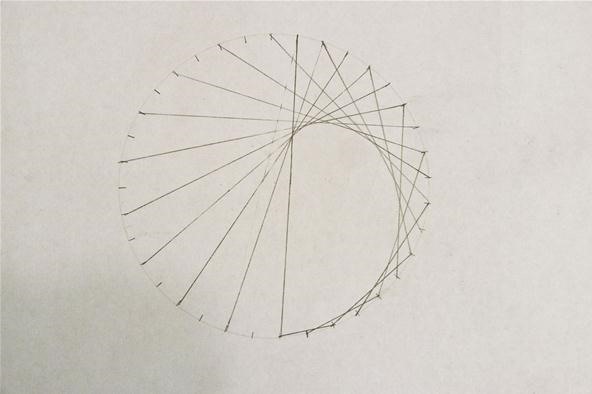
Footstep 2: Skip Ahead by 2 Marks

Starting with any one marking, connect a line from information technology to a mark that is two marks away:

Step 3: Count past Ones & Twos

Take the side by side mark later on your starting signal and connect it to the mark that is two beyond the ending point of the concluding marking.

Take the next mark subsequently your starting point and connect it to the mark that is two beyond the ending indicate of the last marking. Repeat. Y'all are basically counting by ones on the starting points, and past twos on the ending points. Keep going and you'll brainstorm to see the curve accept shape:

Step 4: Continue on Other Side

To avert confusion, simply focus on the marking yous're working on: counting by ones for the starting point and by twos for the ending betoken:

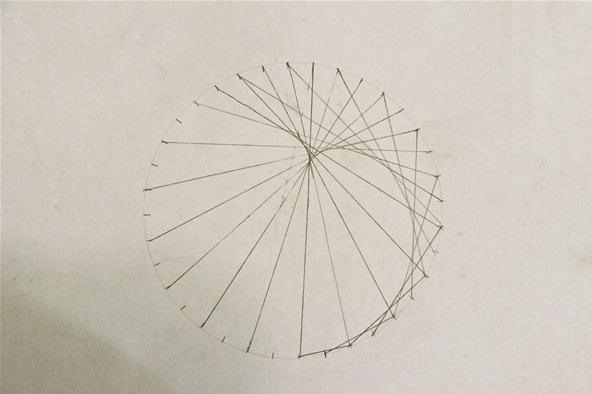
Footstep 5: Stop at Original Starting Point

You'll see the eye take shape once yous become completely around; stop once you return to the commencement mark. My completed cardioid:

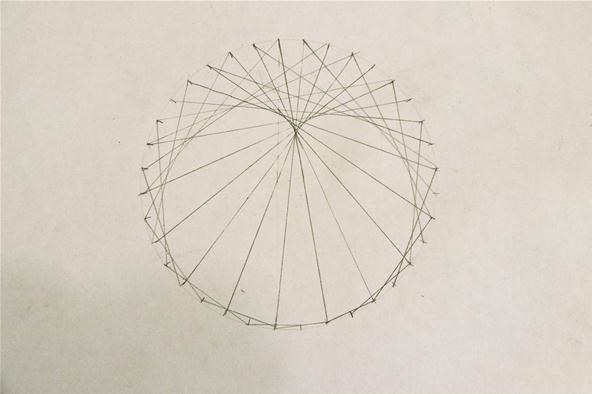
You tin can follow this same process just by counting by threes on the ending marks or fours and you volition become more sharp points. If yous skip less often, you lot volition become a more gradual spiral. The curve beneath was generated past counting by twos just every fourth time.

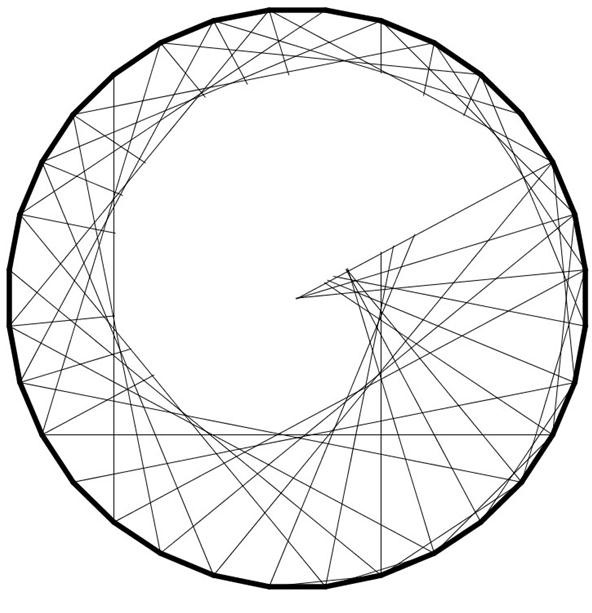
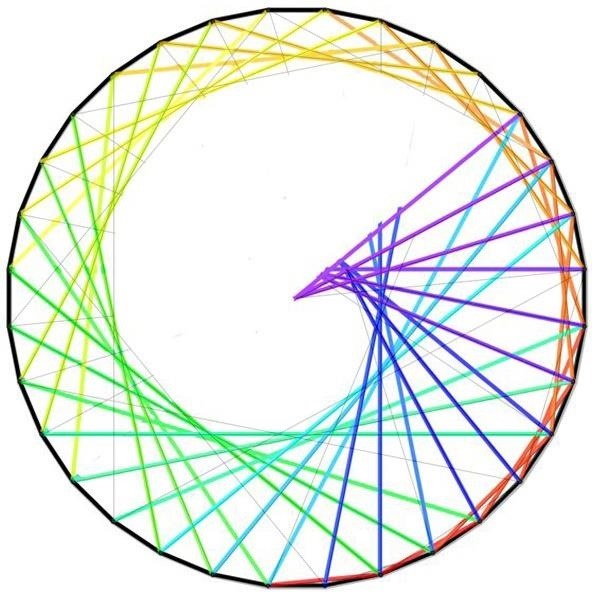
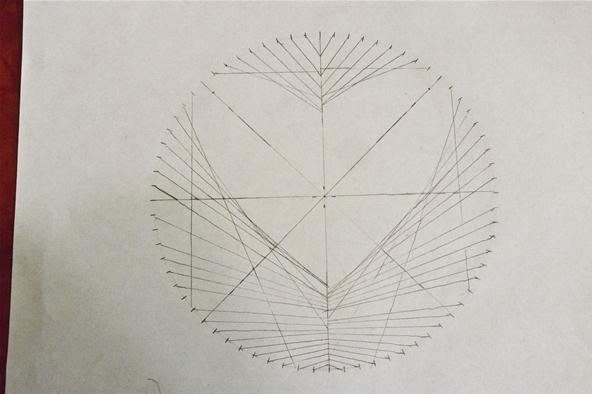
Choice 4. Combine Curves & Create a Middle

Inspired, I decided to endeavor and design a curve that looks more than like a heart by combining linear sections, concentric circle sections, and cardioid sections. I retrieve the concluding blueprint looks pretty good. What do you think?

Step 1: Mark a Circumvolve into Fours

To start, y'all again mark a circle evenly. I chose again 36 marks. I too fabricated the marks at 90 degree intervals more visible; these will be of import markers:

Step 2: Form the Middle's Point

From the bottom, draw a line between two of the marks at xc-degree intervals. This will become part of the pointy end of the heart:

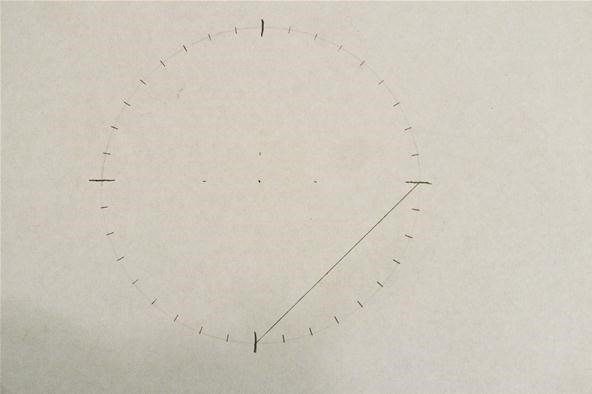
Step iii: Draw Lines for a Concentric Circumvolve

Connect the side by side marks as if you were making the concentric circumvolve design. Stop when you get to the line that connects to the point 180 degrees from the starting betoken. You lot could do the same on the other side. Yous might not desire to do this until y'all are completely washed.

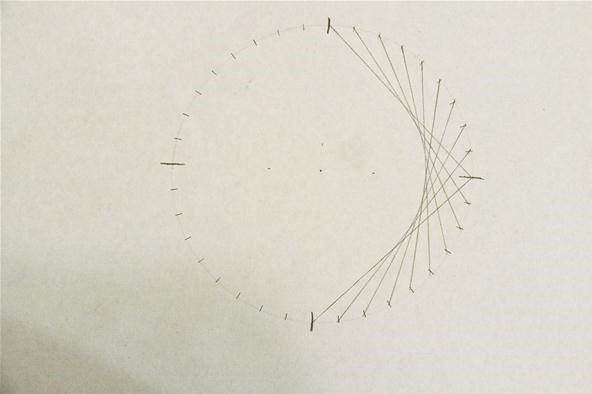
Footstep four: Repeat Process on Other Side

Though nosotros get ahead and complete the concentric-circle design for the opposite side, you can choose to expect until you are completely done with one half in social club to continue all the lines/marks direct:

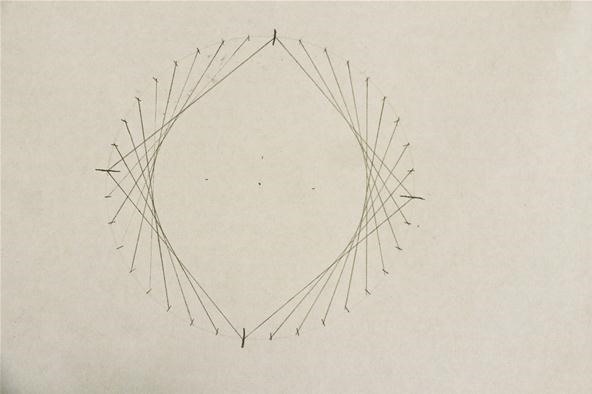
Step 5: Add a Cardioid Section

Next, y'all will add together a cardioid section, starting at the ninety-degree mark correct of the heart's "indicate." From hither, connect marks past counting by ones for the starting betoken of the lines, and by counting by twos for the ending points:

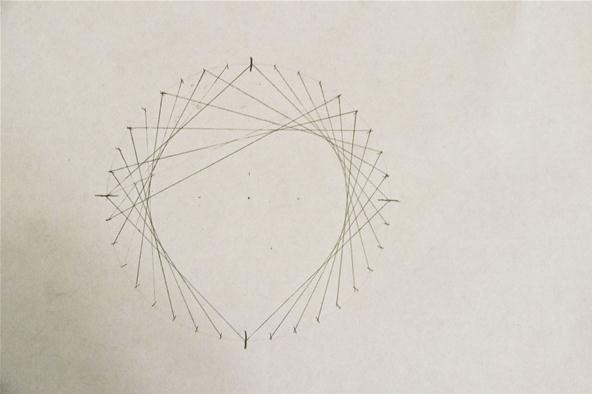
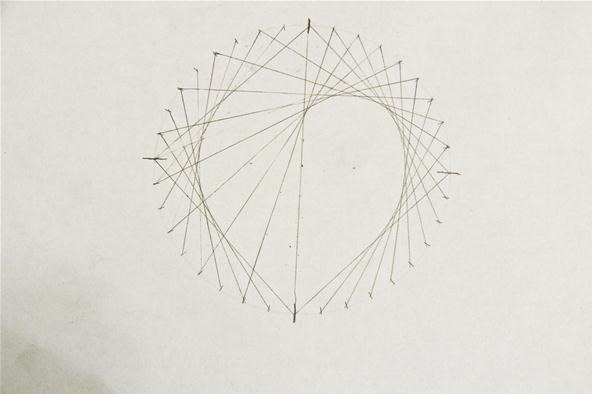
Pace six: Echo on Other Side

With the cardioid department applied to only one-half of the circumvolve, you tin can already run across the centre forming. To finish the "kardioedides," simply repeat the steps for the left side, and your heart is complete!

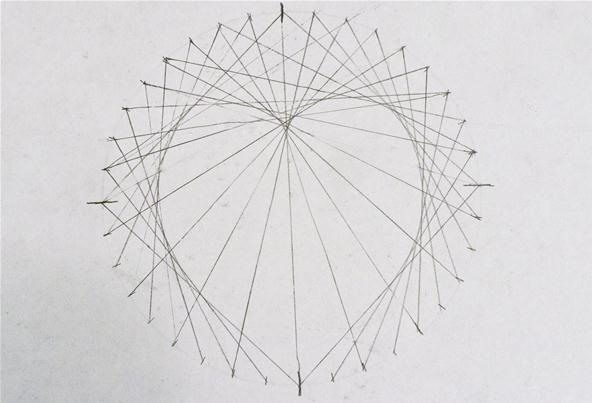
Cool, correct? Finally, from this practice, I took on one more challenge: Using a computer program, I attempted to create the aforementioned heart design using 59 marks instead of 36. I and then colored it in:

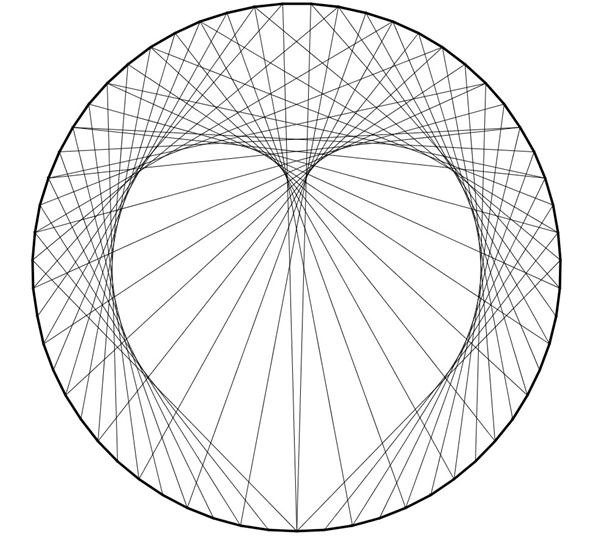
The ideas are pretty fluid when it comes to curves. At present that you're familiar with the basic mathematical curves of the concentric circumvolve, ellipse, and cardioid, you lot, too, tin try your own blueprint ideas. As we've found, with a simple circle and straight lines (and some math logic), yous can create any number of geometric shapes and combinations. What does your eye come across?

Want to primary Microsoft Excel and have your work-from-home task prospects to the next level? Jump-start your career with our Premium A-to-Z Microsoft Excel Training Bundle from the new Gadget Hacks Shop and get lifetime access to more than than xl hours of Basic to Advanced instruction on functions, formula, tools, and more.

Purchase Now (97% off) >

Other worthwhile deals to check out:

97% off The Ultimate 2021 White Hat Hacker Certification Bundle
98% off The 2021 Accounting Mastery Bootcamp Package
99% off The 2021 All-in-1 Data Scientist Mega Bundle
59% off XSplit VCam: Lifetime Subscription (Windows)
98% off The 2021 Premium Learn To Code Certification Bundle
62% off MindMaster Heed Mapping Software: Perpetual License
41% off NetSpot Abode Wi-Fi Analyzer: Lifetime Upgrades